CYK Parsing

在 介绍 PCFG 这篇文章中，我们提到了 parsing。parsing 的任务是根据 grammar 找到句子对应的合适的 parsing tree：

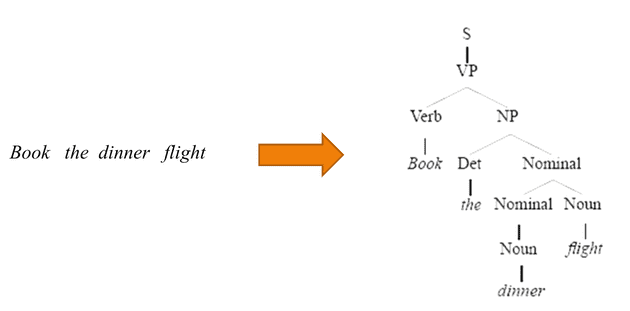
本文介绍的 CYK 算法就是寻找 parsing tree 的一种动态规划算法（CYK 是三个人名字的首字母）。

Chomsky Normal Form

CYK 算法要求使用的 grammar rule 必须遵守 Chomsky 范式（Chomsky Normal Form, CNF）：

1. $X\rightarrow Y_{1}Y_{2} \;\; X,Y_{1},Y_{2}\in N$
2. $X\rightarrow Y\;\;X\in N,Y\in\Sigma$

实际上，任何由上下文无关语法都能由重写规则为 CNF 的语法生成，比如：

可以被重写为下面的 CNF 规则：

因此，CNF 保证了其对应的 parsing tree 是二叉树。

下图是一个 CNF 重写示例：

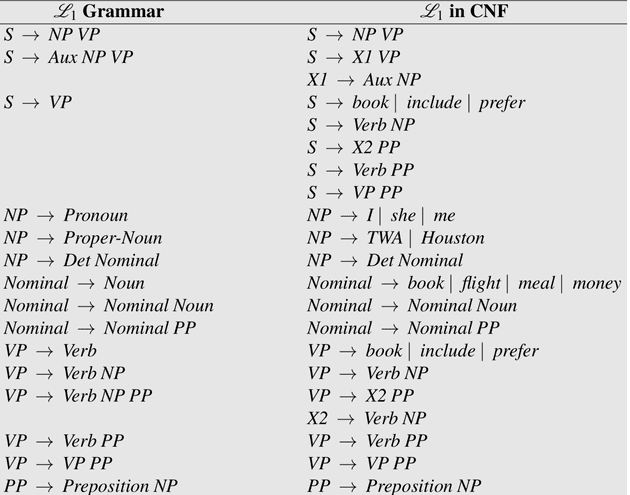
CYK Algorithm

输入：满足 CNF 的 PCFG $G=(N,\Sigma,S,R,q)$，一个句子 $s=x_{1}…x_{n}$ ，其中 $x_{i}$ 代表第 $i$ 个词。

输出为：

也就是 parse tree 概率最大的那句话（以及 parse tree 结构）。

定义 $\mathcal{T}(i,j,X)$ 为以 $X$ 为 parse tree 根节点，扩充到 [i,j] 这几个词所有可能的 parse tree 集合，定义 $\pi(i,j,X)$ 为其中概率最大的 parse tree 对应的概率，那么我们实际上要求的就是 $\pi(1,n,S)$ 。

CYK 算法是自底向上的，因此对于 $i=1…n, X\in N$ 时，有

也就是为最底层与单词有关的规则的概率做初始化，这很容易理解，接下来就是 DP 算法中的状态转移方程：

其中 $(i,j)$ 满足 $1\leq i < j \leq n$ 。

这个方程的意思是说，如果存在 $X\rightarrow Y\;Z$ 这条规则并且 $Y$ 能扩散到 $i$ 和 $s$ 两个词，$Z$ 能扩散到 $s+1$ 和 $j$ 两个词，这样就包括了整句话，因此以 $X$ 为根节点的 parse tree 的概率也能够求得，由于可能有多种可能，因此要取最大值。

这里有一个 CYK 算法的在线 demo，CYK demo。

整个过程的伪代码如图：

References

• http://www.cs.columbia.edu/~mcollins/courses/nlp2011/notes/pcfgs.pdf
• Speech and Language Processing, chapter 12