概率上下文无关语法(PCFG)

在 NLP 任务中，我们可以根据一组 grammar 规则来生成一个句子。

下面这个 grammar 例子表示，一个句子能够由名词短语 I 和动词短语 want a morning filght 组成；名词短语能够由代词 I 组成，或由名词 Los Angeles 组成等。

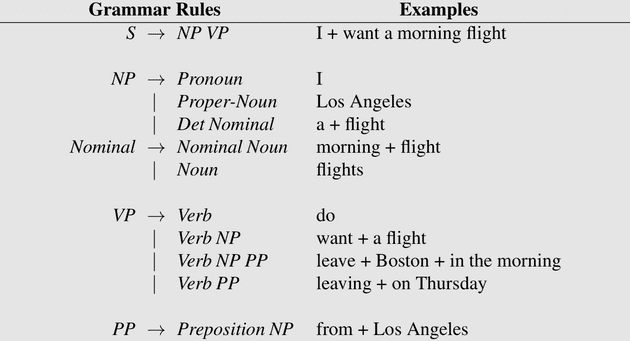
Context-Free Grammar(CFG)

什么是“上下文无关”？

考虑下图这个 parse tree（语法树）：

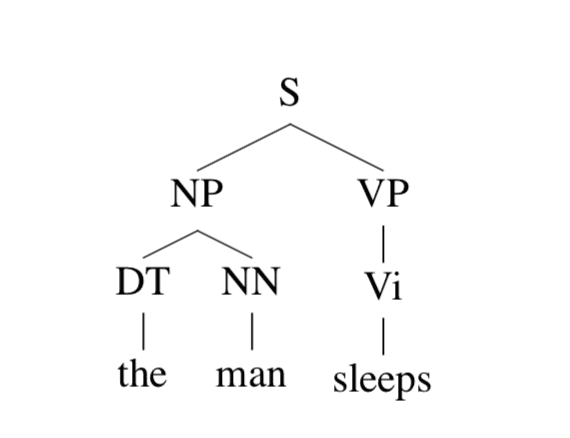
我们来模拟一下这句话生成的过程：

1. S $\rightarrow$ NP VP
2. S $\rightarrow$ NP VP $\rightarrow$ DT NN VP
3. S $\rightarrow$ NP VP $\rightarrow$ DT NN VP $\rightarrow$ the NN VP
4. S $\rightarrow$ NP VP $\rightarrow$ DT NN VP $\rightarrow$ the NN VP $\rightarrow$ the man VP
5. S $\rightarrow$ NP VP $\rightarrow$ DT NN VP $\rightarrow$ the NN VP $\rightarrow$ the man VP $\rightarrow$ the man Vi
6. S $\rightarrow$ NP VP $\rightarrow$ DT NN VP $\rightarrow$ the NN VP $\rightarrow$ the man VP $\rightarrow$ the man sleeps

在第一步到第二步时，DT 和 NN 的生成只与 NP 有关（根据 NP $\rightarrow$ DT NN 这条规则），而与 VP 无关，也就是说，所有规则的左侧只有一个符号，这种形式称为上下文无关。

CFG 定义

CFG 由一个四元组 $N$，$\Sigma$，$R$，$S$ 组成。其中，

• $N$ 是 non-terminal 符号的集合，理解为语法树中的非叶节点（S、NP……）
• $\Sigma$ 是 terminal 符号的集合，也就是各个单词（叶节点 the、man、sleeps）
• $R$ 代表 grammar 中的规则，如 S$\rightarrow$ NP VP
• $S$ 代表开始的标记，也就是语法树的根节点

上面例子的语法树是根据下面这个 grammar 生成的。由一句话和一个 grammar 生成 parse tree 的过程叫做 parsing。在这里由于句子是由 grammar 生成的，这种建模方法也被称为 generative grammar。

现在我们使用这个 grammar 来生成这样一句话：the man saw the dog with the telescope，会产生什么样的 parse tree 呢？

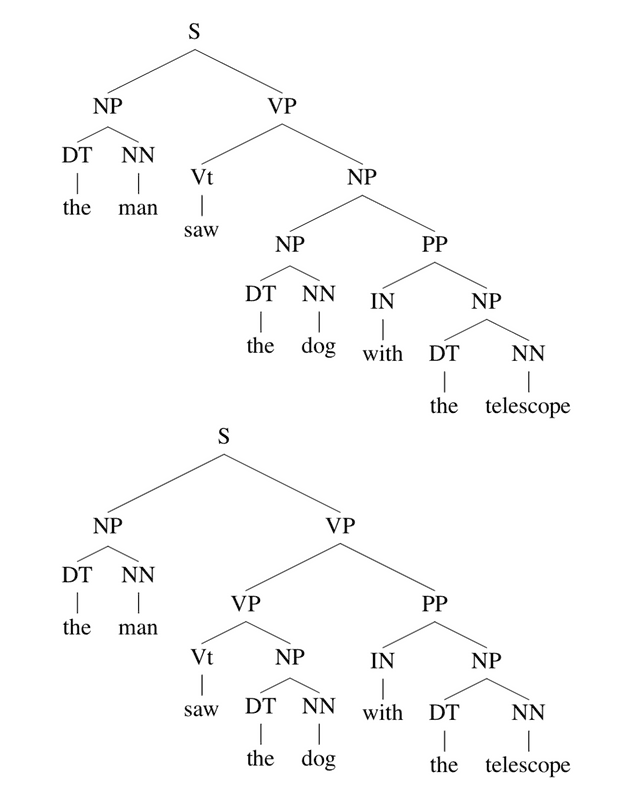
看，两个 parse tree 都是有效的，但却是两种语义。为了解决这种歧义的现象，我们在 CFG 中引入了概率的概念。

Probabilistic Context-Free Grammar(PCFG)

给定一个上下文无关语法 $G$，称 $\mathcal{T}_{G}$ 为 grammar $G$ 下的所有 parse tree 的集合，简写为 $\mathcal{T}$。那么就有

因此如果知道了概率分布 $p(t)$，那么我们就可以通过排序找到一句话最有可能的 parse tree。

PCFG 定义

1. 一个上下文无关语法 $G=(N,\Sigma,S,R)$
2. 对应每个规则 $\alpha\rightarrow\beta\in R$ 的概率为 $q(\alpha\rightarrow\beta)$，实际上这是在给定$\alpha$ 为规则左侧符号时，$\alpha\rightarrow\beta$ 这条规则的条件概率。因此在任意 $X\in N$ 时，有

因此，如果一个 parse tree $t\in\mathcal{T}_{G}$ 包含$\alpha_{1}\rightarrow\beta_{1},\alpha_{2}\rightarrow\beta_{2},…,\alpha_{n}\rightarrow\beta_{n}$这些规则，那么 $t$ 在 PCFG 下的概率为

上图为一个 PCFG，可以验证其满足

如果 parse tree 是这样：

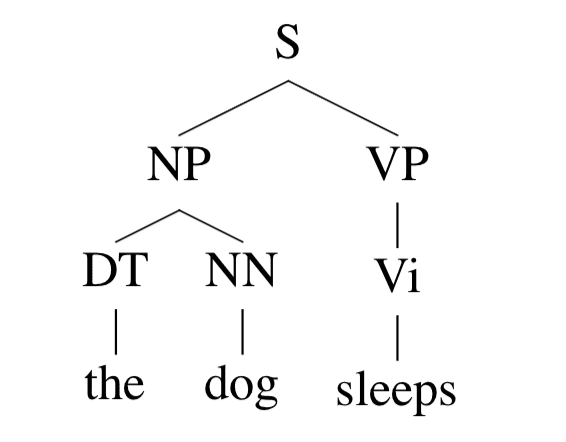
那么这个 parse tree 的概率就是

References

• http://www.cs.columbia.edu/~mcollins/courses/nlp2011/notes/pcfgs.pdf
• Speech and Language Processing, chapter 11