The Inside-Outside Algorithm

October 28, 2017

上篇文章中介绍了一种 parsing 算法 CYK，这篇文章要介绍的 inside-outside 是另一个 parsing 算法。

算法输入

什么是 potential function？

对于一个规则 $r$ ，使用 $\psi(r)$ 代表这个规则的 potential，在这里也就是概率：

\psi(A\rightarrow B \; C,i,k,j)=q(A\rightarrow B \; C)

\psi(A,i)=q(A\rightarrow x_{i})

因此对于一个 parse tree t ，它的概率为 $\psi(t)=\prod_{r\in t}\psi(r)$ .

$Z=\sum_{t\in \mathcal{T}}\psi{(t)}$ 表示所有可能的 parse tree 的概率和。

对于所有规则 $r$ , 定义

\mu(r)=\sum_{t\in\mathcal(T):r\in t} \psi(t)

也就是所有包括规则 $r$ 的 parse tree 概率和。

以及对于 $A\in N, 1 \leq i \leq j \leq n$ ，

\mu(A,i,j) = \sum_{t\in\mathcal(T):(A,i,j)\in t}\psi(t)

也就是所有 parse tree 中，以 $A$ 为根节点，叶节点扩散到 $x_{i}…x_{j}$ 这些单词的子树的概率和。

我们使用 $\alpha(A,i,j)$ 和 $\beta(A,i,j)$ 分别代表 inside 和 outside 算法。

inside 算法实际上就是把 CYK 中对所有 parse tree 取最大概率的操作换成了求和。

即

\alpha(A,i,j)=\sum_{t\in \mathcal{T}(A,i,j)}\psi(t)

以这个 parse tree 为例：

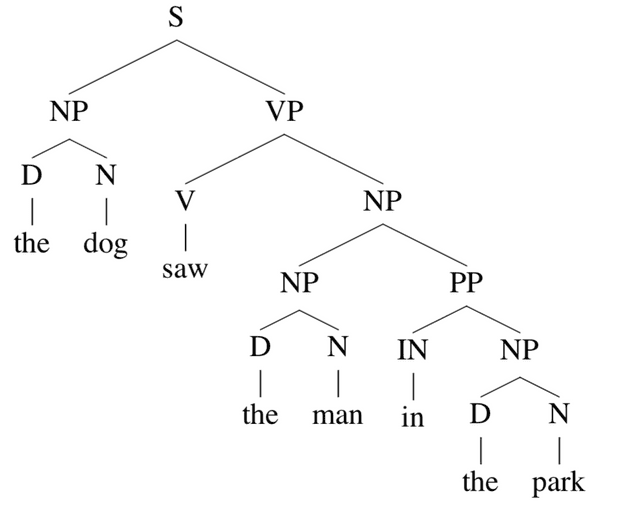
它关于 $(\mathrm{NP},4,5)$ 的 inside tree $t_{2}$ 就是

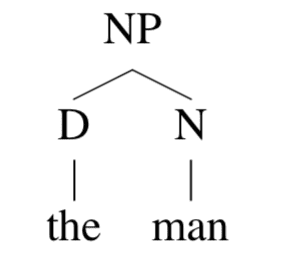
同样地，outside tree $t_{1}$ 是

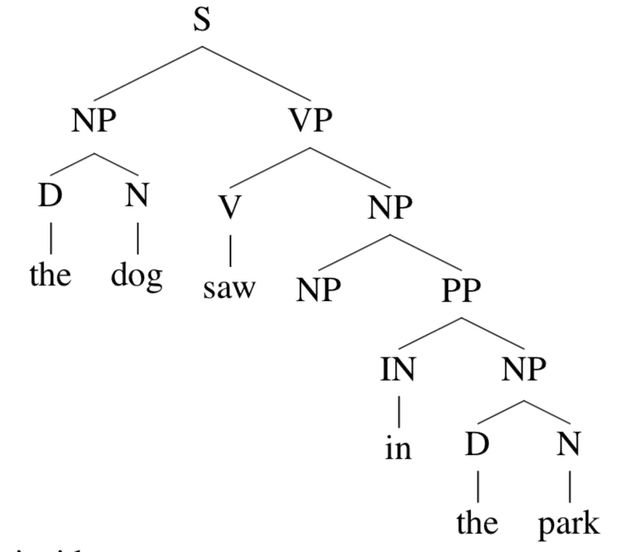
这个 outside tree 根节点是 $S$ ，叶节点是 $x_{1}…x_{3} \; \mathrm{NP} \; x_{6}…x_{n}$

易知

\psi(t)=\psi(t_{1})\times \psi(t_{2})

由上述定义知，对于一个 outside tree $t$ ，它的 potential 为 $\psi(t)$ ，也就是这个 tree 里所有规则的乘积。

我们使用符号 $\mathcal{O}(A,i,j)$ 来代表所有可能的 outside tree 的集合（以 $A$ 为根节点，扩散到 $i$ 和 $j$ 之间的所有单词），那么

\beta(A,i,j) = \sum_{t\in \mathcal{O}(A,i,j))}\psi(t)

也就是说， $\beta(A,i,j)$ 是所有 $\mathcal{O}(A,i,j)$ 中 potential 的和。

根据上述定义推出一些性质：

Z=\sum_{t\in \mathcal{T}}\psi{(t)}=\alpha(S,1,n)

\begin{aligned} \mu(A, i, j) &=\sum_{t \in \mathcal{T}:(A, i, j) \in t} \psi(t) \\ &=\sum_{t_{1} \in \mathcal{O}(A, i, j)} \sum_{t_{2} \in \mathcal{T}(A, i, j)}\left(\psi\left(t_{1}\right) \times \psi\left(t_{2}\right)\right) \\ &=\left(\sum_{t_{1} \in \mathcal{O}(A, i, j)} \psi\left(t_{1}\right)\right) \times\left(\sum_{t_{2} \in \mathcal{T}(A, i, j)} \psi\left(t_{2}\right)\right) \\ &=\alpha(A, i, j) \times \beta(A, i, j) \end{aligned}

Inside-outside 算法的全部过程如图：

在掷硬币中的 EM 算法中我们介绍了 EM 算法，EM 算法在 PCFG 中起着非常重要的作用，它的实质是参数的更新。

算法的输入有 $n$ 个训练样本（n 句话），例如 $x^{(i)}_{1}$ 代表第 $i$ 个样本中的第一个单词。

设 $\mathcal{T}_{i}$ 为第 $i$ 轮迭代时所有可能的 parse tree， $q(r)$ 为规则 $r$ 的参数（概率），

初始 $q^{0}(r)$ 可以设为随机值，然后算出 $q^{1},q^{2},…$ 直到收敛。

$q$ 的更新过程如下，首先需要算出在 $t-1$ 次迭代时 $q^{t-1}$ 下的 expected counts $f(r)$ ，那么 $q^{t}$ 就能求得：

q^{t}(A\rightarrow\gamma)=\dfrac{f(A\rightarrow \gamma)}{\sum_{A\rightarrow\gamma\in R}f(A\rightarrow\gamma)}

那么如何计算 $f(r)$ 呢？

设 $\mathrm{count}(t,r)$ 为规则 $r$ 出现在 $t$ 中的次数， $\underline{\theta}$ 是代表所有规则概率的 vector，那么有

f^{t-1}(r)=\sum^{n}_{i=1} \sum_{t\in \mathcal{T}_{i} } p(t|x^{i};\underline{\theta}^{t-1})\mathrm{count}(t,r)

第一个求和代表所有的训练样本，对于每个训练样本，再求和所有可能的 parse tree。对于每个 parse tree，将条件概率与 count 二者相乘。

因此对于单个训练样本，

\mathrm{count}(r)=\sum_{t\in \mathcal{T}_{i} } p(t|x^{i};\underline{\theta}^{t-1})\mathrm{count}(t,r)

可以使用 inside-outside 算法计算 $\mathrm{count}(r)$ ，如图：