常用激活函数的总结与比较

February 05, 2017

本文为 CS231n 中关于激活函数部分的笔记。

激活函数（Activation Function）能够把输入的特征保留并映射下来。

Sigmoid

Sigmoid 非线性函数将输入映射到 $\left( 0,1\right)$ 之间。它的数学公式为： $\sigma \left( x\right) =\dfrac {1} {1+e^{-x}}$ 。

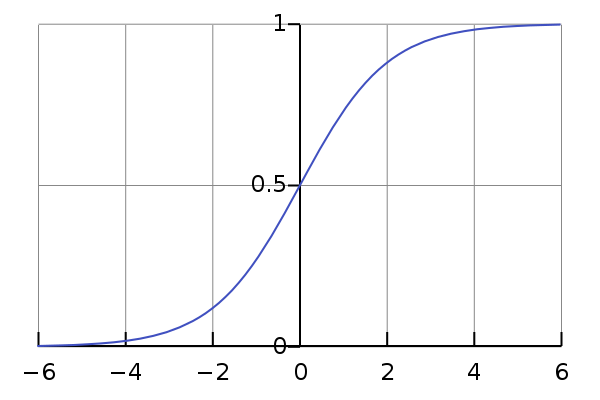
历史上，sigmoid 函数曾非常常用，然而现在它已经不太受欢迎，实际很少使用了，因为它主要有两个缺点：

1. 函数饱和使梯度消失

sigmoid 神经元在值为 0 或 1 的时候接近饱和，这些区域，梯度几乎为 0。因此在反向传播时，这个局部梯度会与整个代价函数关于该单元输出的梯度相乘，结果也会接近为 0 。

这样，几乎就没有信号通过神经元传到权重再到数据了，因此这时梯度就对模型的更新没有任何贡献。

除此之外，为了防止饱和，必须对于权重矩阵的初始化特别留意。比如，如果初始化权重过大，那么大多数神经元将会饱和，导致网络就几乎不学习。

2. sigmoid 函数不是关于原点中心对称的

这个特性会导致后面网络层的输入也不是零中心的，进而影响梯度下降的运作。

因为如果输入都是正数的话（如 $f=w^{T}x+b$ 中每个元素都 $x>0$ ），那么关于 $w$ 的梯度在反向传播过程中，要么全是正数，要么全是负数（具体依据整个表达式 $f$ 而定），这将会导致梯度下降权重更新时出现 z 字型的下降。

当然，如果是按 batch 去训练，那么每个 batch 可能得到不同的信号，整个批量的梯度加起来后可以缓解这个问题。因此，该问题相对于上面的神经元饱和问题来说只是个小麻烦，没有那么严重。

tanh

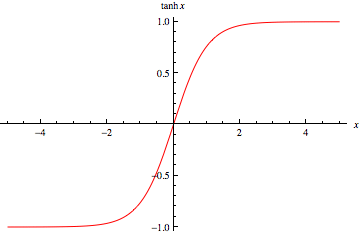
tanh 函数同样存在饱和问题，但它的输出是零中心的，因此实际中 tanh 比 sigmoid 更受欢迎。

tanh 函数实际上是一个放大的 sigmoid 函数，数学关系为： $\tanh \left( x\right) =2\sigma \left( 2x\right) -1$

ReLU

ReLU 近些年来非常流行。它的数学公式为： $f\left( x\right) =\max \left( 0,x\right)$ 。

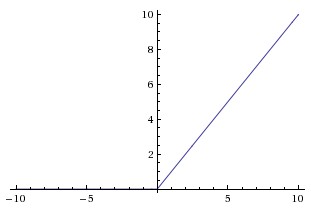
$w$ 是二维时，ReLU 的效果如图：

ReLU 的优点：

相较于 sigmoid 和 tanh 函数，ReLU 对于 SGD 的收敛有巨大的加速作用（Alex Krizhevsky 指出有 6 倍之多）。有人认为这是由它的线性、非饱和的公式导致的。
相比于 sigmoid/tanh，ReLU 只需要一个阈值就可以得到激活值，而不用去算一大堆复杂的（指数）运算。

ReLU 的缺点是，它在训练时比较脆弱并且可能“死掉”。

举例来说：一个非常大的梯度经过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了。如果这种情况发生，那么从此所有流过这个神经元的梯度将都变成 0。

也就是说，这个 ReLU 单元在训练中将不可逆转的死亡，导致了数据多样化的丢失。实际中，如果学习率设置得太高，可能会发现网络中 40% 的神经元都会死掉（在整个训练集中这些神经元都不会被激活）。

合理设置学习率，会降低这种情况的发生概率。

Leaky ReLU

Leaky ReLU 是为解决“ ReLU 死亡”问题的尝试。

ReLU 中当 x<0 时，函数值为 0。而 Leaky ReLU 则是给出一个很小的负数梯度值，比如 0.01。

有些研究者的论文指出这个激活函数表现很不错，但是其效果并不是很稳定。

Kaiming He 等人在 2015 年发布的论文 Delving Deep into Rectifiers 中介绍了一种新方法 PReLU，把负区间上的斜率当做每个神经元中的一个参数来训练。然而该激活函数在在不同任务中表现的效果也没有特别清晰。

Maxout

Maxout 是对 ReLU 和 Leaky ReLU 的一般化归纳，它的函数公式是（二维时）： $\max \left( w_{1}^{T}+b_{1},W_{2}^{T}+b_{2}\right)$ 。ReLU 和 Leaky ReLU 都是这个公式的特殊情况（比如 ReLU 就是当 $w_{1},b_{1}=0$ 时）。

这样 Maxout 神经元就拥有 ReLU 单元的所有优点（线性和不饱和），而没有它的缺点（死亡的 ReLU 单元）。然而和 ReLU 对比，它每个神经元的参数数量增加了一倍，这就导致整体参数的数量激增。

如何选择激活函数？

通常来说，很少会把各种激活函数串起来在一个网络中使用的。

如果使用 ReLU，那么一定要小心设置 learning rate，而且要注意不要让你的网络出现很多 “dead” 神经元，如果这个问题不好解决，那么可以试试 Leaky ReLU、PReLU 或者 Maxout.

最好不要用 sigmoid，可以试试 tanh，不过可以预期它的效果会比不上 ReLU 和 Maxout.